一个价值万亿的数学公式：从物理方程到金融期权定价¶

从物理与数学到金融市场¶

你可能难以置信，一个源于物理与数学的方程竟然能催生多个总规模达数万亿美元的金融产业链时。然而，这正是现代金融史中的真实故事。期权（Options） 的定价理论与技巧，深受数学、统计、物理以及概率论的影响。通过探索这一交叉领域，我们不但能了解期权定价的起源，更能窥见量化金融如何从理论走向实践，进而改变全球资本市场的运作方式。

期权的概念与风险管理¶

期权是一种给持有人在未来以特定价格买入或卖出某资产的“权利，但非义务”的金融合约。以欧式看涨期权（Call Option）为例：

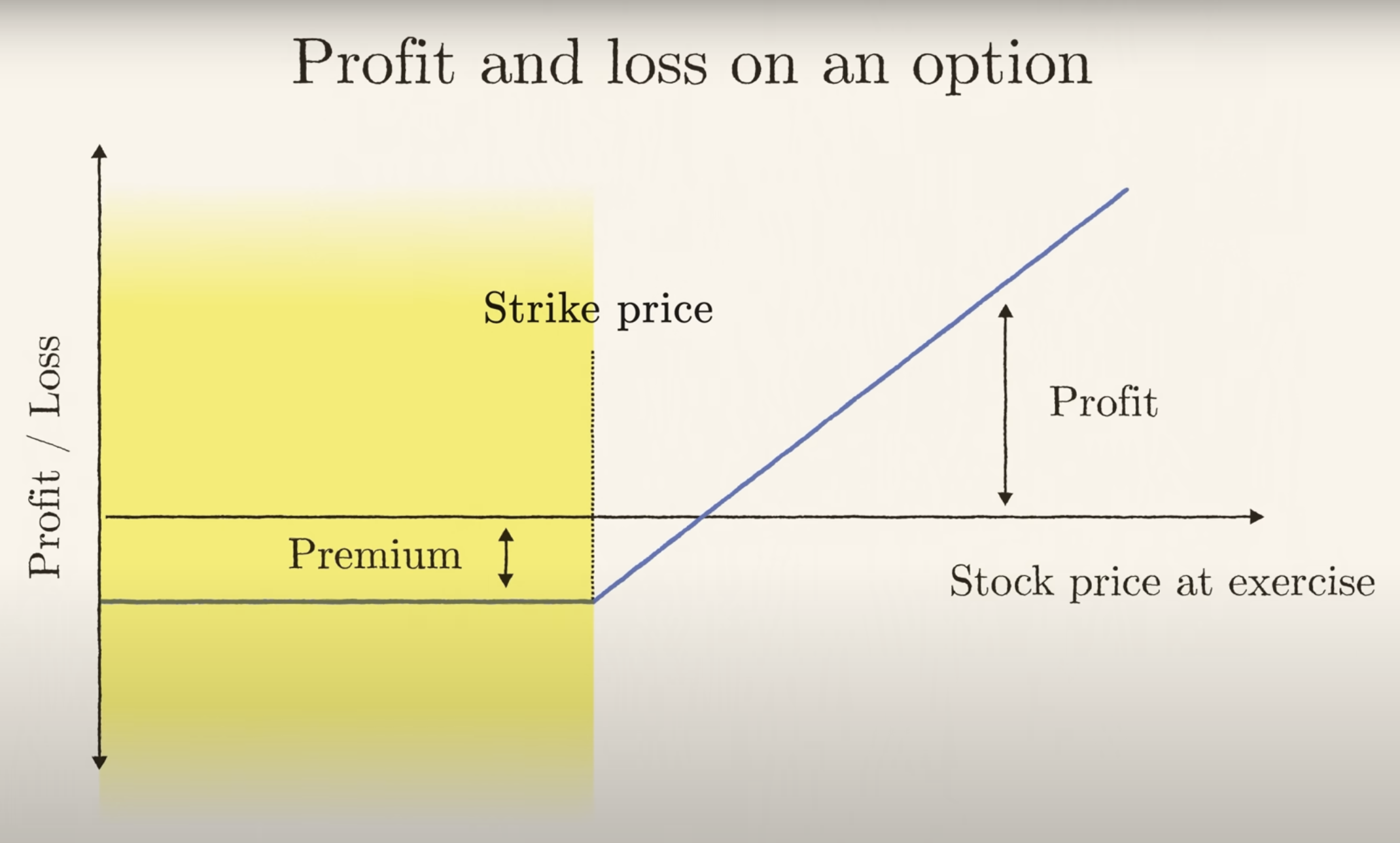
当前标的资产价格为 \(S_0\)
行权价（执行价）为 \(K\)
到期日为 \(T\)
若到期时标的价格 \(S_T > K\)，则期权多头可获利 \(\max(S_T - K,0)\)；
若 \(S_T \leq K\)，则期权多头选择不执行，损失仅为最初支付的期权费。

这种合约形式早在公元前600年就被古希腊哲学家泰勒斯（Thales） 运用过。他通过支付少量费用提前锁定橄榄榨油机的使用权，一旦橄榄大丰收，他便能从中获利。这种先见之明的风险与机会管理思维，正是期权设计背后的基本逻辑。

从随机漫步到期权定价：巴舍利耶的先驱之举¶

早期的期权交易全凭交易员的经验和直觉定价。直到1900年，法国数学家路易·巴舍利耶（Louis Bachelier）在其博士论文中提出：股价未来的运动可视为对称的随机过程。他假设在短时间间隔 \(\Delta t\) 内，股价变动 \(\Delta S\) 满足：

\[ \Delta S \sim \sigma \sqrt{\Delta t} Z \]

其中 \(\sigma\) 为波动率，\(Z\) 为标准正态随机变量。当时间推移，价格变动累积后，股价 \(S_T\) 的分布趋近正态：

\[ S_T \sim \mathcal{N}(S_0, \sigma^2 T) \]

（这是巴舍利耶原始模型的假设，后经改良为对数正态模型。）

通过计算各种未来价格发生的概率，并令期权买卖双方的期望收益相等，巴舍利耶给出了期权的“公平价格”概念。可惜当时这一革命性思想未引起足够关注。

布朗运动与爱因斯坦的启示¶

有趣的是，巴舍利耶的随机漫步思想与物理学中布朗运动（Brownian Motion）的研究如出一辙。1905年，爱因斯坦证明悬浮微粒的无序运动来自无数无法预测的分子撞击。这在数学上可用维纳过程（Wiener Process）描述：

\[ X_t = X_0 + W_t, \quad W_t \sim \mathcal{N}(0,t) \]

爱因斯坦的研究间接证明了分子真实存在，并为随机过程提供了坚实的物理基础。这种随机性模型与金融价格的不可预测性不谋而合。

从赌桌到华尔街：数学策略的进化¶

20世纪中叶，Ed Thorp通过数学策略在赌场的二十一点游戏中获利，然后将类似思路用于股市。他以 “对冲”（Hedging） 概念为核心，通过动态调整标的资产与期权头寸的比例（Delta Hedging）来降低风险。例如，当持有卖出的看涨期权时，为消除标的价格上涨带来的损失，可对应持有部分标的资产，使总体风险趋近中性。

Black-Scholes-Merton：期权定价的经典方程¶

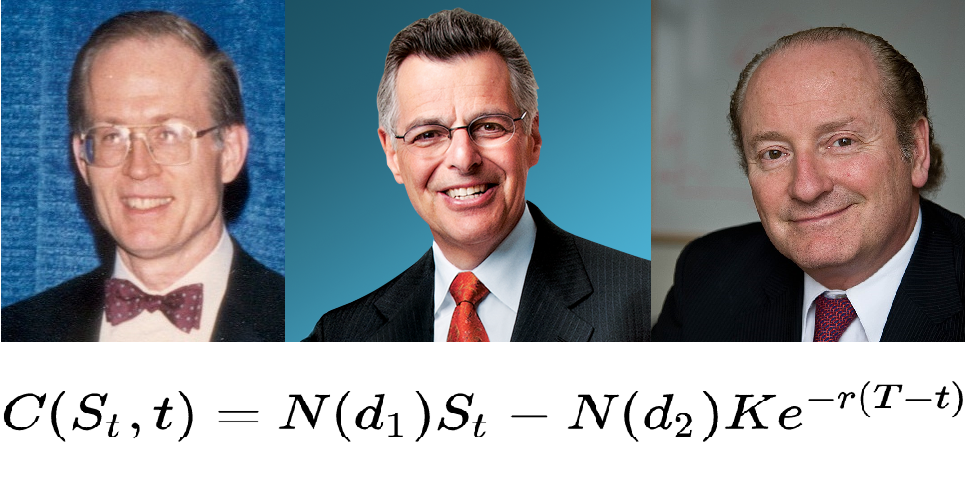
1973年，费雪·布莱克（F. Black）、迈伦·斯科尔斯（M. Scholes）和罗伯特·默顿（R. Merton）提出了著名的Black-Scholes公式。在该模型中，股价被设为服从几何布朗运动：

\[ S_T = S_0 e^{(r - \frac{\sigma^2}{2})T + \sigma\sqrt{T}Z} \]

其中 \(\(r\)\) 为无风险利率。对于欧式看涨期权，Black-Scholes定价公式为：

\[ C_0 = S_0 N(d_1) - K e^{-rT}N(d_2) \]

其中

\[ d_1 = \frac{\ln(\frac{S_0}{K}) + (r+\frac{\sigma^2}{2})T}{\sigma\sqrt{T}}, \quad d_2 = d_1 - \sigma \sqrt{T} \]

\(\(N(\cdot)\)\) 为标准正态分布的累积分布函数。

Black-Scholes模型为期权定价提供了清晰可计算的标准，促使期权市场快速增长，进而催生了信贷违约掉期、场外衍生品、资产证券化等万亿美元级产业。

对冲与杠杆的双面性¶

有了明确定价公式，企业与投资者可利用期权和衍生品精准对冲风险。例如，航空公司若担心油价上涨，可购入与油价相关的期权锁定成本。同时，期权提供杠杆效应，让投资者用较少资金获得更大敞口。然而，这种杠杆也会在市场波动时放大风险。正常时期，丰富的衍生品增强市场流动性与稳定性；极端动荡中，高度相关的崩盘会通过衍生品市场加剧整体风险。

量化帝国的崛起：吉姆·西蒙斯与文艺复兴科技¶

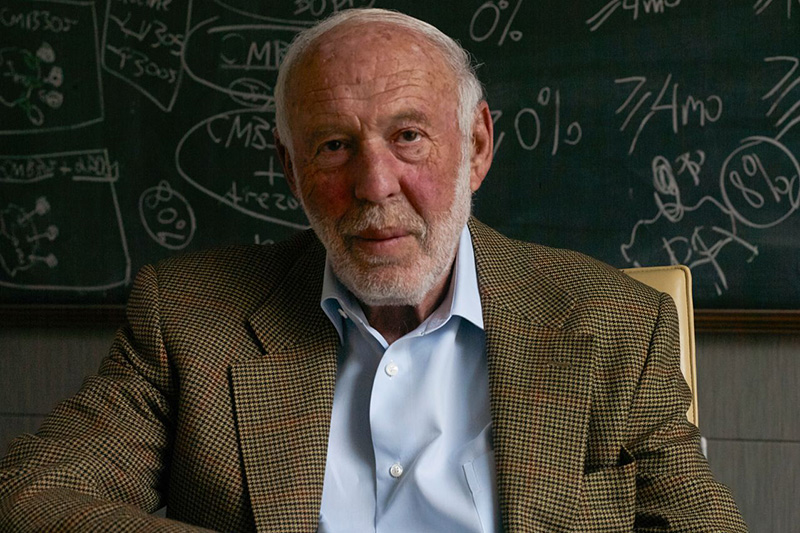
Black-Scholes公式公开后，简单套利机会渐少。以吉姆·西蒙斯（Jim Simons）为首的一批数学家、物理学家，利用更复杂的统计与机器学习方法，从海量数据中挖掘微小但持久的价格模式。文艺复兴科技公司（Renaissance Technologies）的Medallion基金年均回报率高达66%，令人瞠目，这对市场有效性提出质疑，也彰显了高精尖数学工具的威力。

完美效率的悖论¶

当越来越多的学者和从业者使用数学模型与算法挖掘市场模式，市场变得更有效率，套利空间更难寻找。理论上，若所有价格规律被穷尽，市场价格将真正成为随机漫步，从而再无轻易盈利的机会。这是量化金融的悖论：我们用数学逼近完美市场，同时也在不断减少下一代投资者获取超额收益的潜能。

结语¶

从巴舍利耶的期权定价雏形，到爱因斯坦的布朗运动，再到Black-Scholes公式的问世与广泛应用，数学与物理为金融市场提供了理解与定价风险的思路。量化金融让风险管理工具更加完善，创造万亿美元级市场。然而，随着市场朝有效率和透明化方向发展，不断提高的“智力门槛”也减少了套利机会。

在无限逼近完美的道路上，我们见证了科学与金融交织下的伟大创造与自我调适。这正是量化金融的魅力所在：它的终点，也许是一个无差别的随机世界，但在到达终点的过程中，人类以数学和科学之名，彻底改写了金融的游戏规则。

如果您对人工智能和量化金融的结合感兴趣，欢迎加入LLMQuant社区，共同探索人工智能在量化投资领域的应用。

关于LLMQuant¶

LLMQuant是由一群来自世界顶尖高校和量化金融从业人员组成的前沿社区，致力于探索人工智能（AI）与量化（Quant）领域的无限可能。我们的团队成员来自剑桥大学、牛津大学、哈佛大学、苏黎世联邦理工学院、北京大学、中科大等世界知名高校，外部顾问来自Microsoft、HSBC、Citadel、Man Group、Citi、Jump Trading、国内顶尖私募等一流企业。