你真的读懂夏普比率？量化交易员带你入门Sharpe Ratio¶

大家好，欢迎来到这篇关于夏普比率（Sharpe Ratio）的科普推文。本文帮助你更系统、深入地理解夏普比率在量化投资和投资组合管理中的重要作用，以及专业的量化交易员如何看待Sharpe Ratio。

1. 为什么不能只看收益率？¶

在直觉上，我们常常把"收益率"视为衡量一个投资好坏的核心指标，但现实投资中，"收益率"只是故事的一半。

案例：绿色投资 vs. 黑色投资

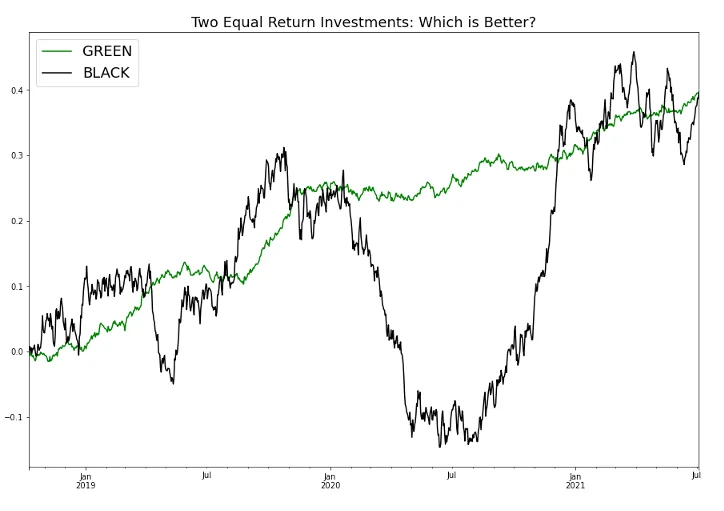
绿色投资：最终总收益 40%，过程相对平稳
黑色投资：最终总收益同样是 40%，但曲线剧烈波动

两者最终收益看似相同，却并不代表它们"质量"一致。黑色投资过程中大起大落，带来以下问题： 1. 心理压力：如若中途出现大回撤，投资人会恐慌，甚至可能提前割肉。 2. 信心不足：波动越大，未来越难预测；而平稳向上的绿色更具可预期性。 3. 流动性需求：万一在黑色投资大幅回撤时需要现金，就可能不得不在较低价位卖出，造成实际亏损。

结论：在拥有同样"最终收益"的情况下，更稳定的投资显然更受欢迎。这就引出了"风险调整后收益"的概念——我们需要让"波动"或"风险"在回报测度中占有一席之地。

2. 用波动率量化"风险"¶

要想在衡量回报时考虑风险，先得量化风险。标准差（Standard Deviation）或波动率（Volatility）便是投资中最常见的风险度量方式，记作 \(\sigma\)。

其数学定义为：

\[ \sigma = \sqrt{\frac{1}{n-1} \sum_{t=1}^{n} \bigl(r_t - \bar{r}\bigr)^2} \]

\(r_t\)：投资在第 \(t\) 个时段的收益率
\(\bar{r}\)：收益率的平均值
\(n\)：统计的周期数（如天、周、月等）

通俗地说，波动率就是"收益围绕均值的偏离程度"。波动率越大，说明投资的"走向"越不稳定，风险也越高。

3. 夏普比率（Sharpe Ratio）的定义¶

当我们有了"波动率"这个衡量风险的工具后，就能定义"风险调整后收益"——即"夏普比率（Sharpe Ratio）"。

3.1 一般形式¶

从理论上讲，夏普比率最常见的公式是：

\[ \text{Sharpe Ratio} = \frac{\bar{r} - r_f}{\sigma} \]

\(\bar{r}\)：投资的平均收益率
\(r_f\)：无风险收益率（Risk-Free Rate），在某些案例中可能省略或简化
\(\sigma\)：投资收益的波动率

不过，在不少量化交易实务中，尤其是短周期（例如日度数据）时，很多人会暂时忽略 \(r_f\)，或者令 \(r_f \approx 0\)。于是，就得到了更简化的形式：

\[ \text{Sharpe Ratio} = \frac{\bar{r}}{\sigma} \]

3.2 年化夏普比率¶

为了方便比较，有时我们还会把夏普比率"年化"。若使用日度数据，通常会乘以 \(\sqrt{252}\)（约 252 个交易日）：

\[ \text{Sharpe Ratio (annualized)} = \frac{\bar{r}_{\text{daily}}}{\sigma_{\text{daily}}} \times \sqrt{252} \]

若使用月度数据，则可乘以 \(\sqrt{12}\) 来年化，以此类推。

3.3 它好在哪？¶

收益越高，夏普比率越高：反映了收益对指标的正贡献。
波动越大，夏普比率越低：越不平稳的投资，被"惩罚"得更严重。

所以，夏普比率一举两得：既能鼓励高回报，也能约束高风险。

4. 夏普比率的直观例子¶

回到最开头"绿色 vs. 黑色"的例子：
- 如果我们为绿色计算夏普比率，假设结果是 2
- 为黑色计算，假设结果只有 0.5
- 在回报同为 40% 的前提下，夏普比率清晰地显示"绿色优于黑色"

原因：绿色更平稳，承担更少的风险就拿到了与黑色相同的收益。

5. 如何通过组合提升夏普比率？¶

5.1 分散化（Diversification）¶

假设有两个投资： - 红色（Red）
- 蓝色（Blue）

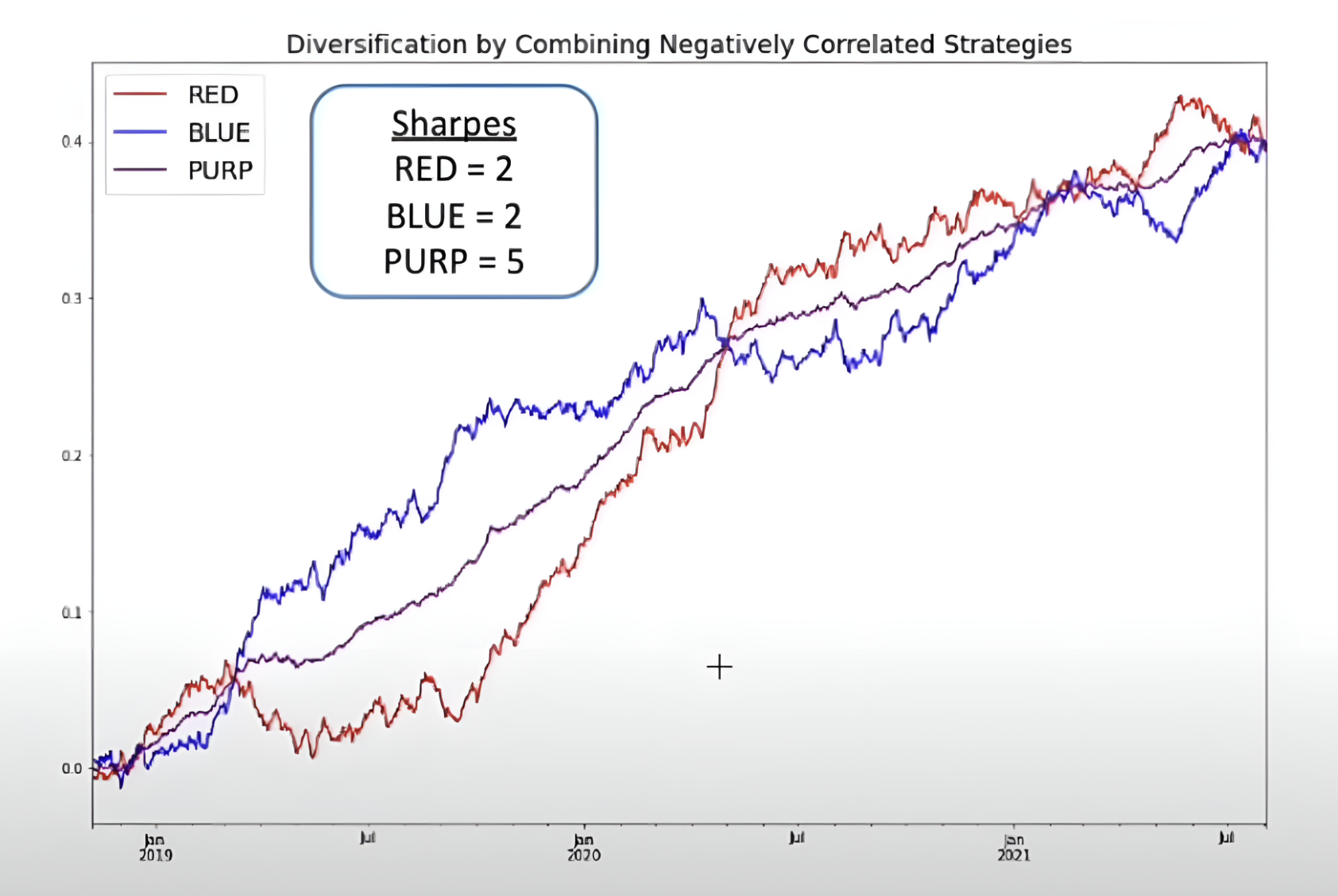它们各自的回报和波动情况相似，且各自的夏普比率都为 2。看上去二者不相上下。但是，倘若二者呈负相关或低相关，当红色上涨时蓝色下跌，或二者走势差异明显，我们可以将这两个投资按照一定权重（例如各 50%）组合在一起，得到一个新的组合（图中用"Perp"代表）。

结果往往令人惊喜： - 红、蓝各自夏普比率为 2
- 二者的混合组合可能夏普比率飙升到 5（甚至更高），收益不变而波动大幅下降

原因：二者在价格波动上部分相互抵消，最终让组合整体曲线更平滑。
启示：这就是"不要把鸡蛋放在同一个篮子里"的量化体现；当我们想"对冲"或"分散投资"时，实则是在努力提升组合的夏普比率。

6. 高夏普 vs. 高回报：杠杆的魔力¶

或许有人说："如果一个策略收益不算最高，但夏普很高；另一个策略收益更大，但夏普一般。选哪个？"

答案：大多数情况下选高夏普策略，并通过杠杆放大。

6.1 杠杆（Leverage）的原理¶

假设你有 100 美元资金： 1. 你再借来 100 美元，用于投资某个标的
2. 这时你的总投资是 200 美元，杠杆倍数 = 2 倍

如果标的上涨 1%，你赚的并不是 1 美元，而是 2 美元；相当于你本金的收益率达 2%
同理，若标的下跌 1%，亏损也会放大为 2 美元

结论：杠杆放大了绝对收益和绝对亏损，但不改变夏普比率。因为随着收益倍率提升，波动也相应成比例提升，两者同时被放大，分子分母的比例并未改变。

6.2 如何用杠杆？¶

先选择一个"基础夏普比率"足够高的策略
如果觉得收益率水平不够，可以把策略加杠杆，以获得更高的"最终收益"
在此过程中，夏普比率基本保持不变（忽略融资成本、滑点、交易成本等现实因素），也就意味着你可以拥有"平稳 + 更高收益"的理想投资线

注意：过度杠杆会带来爆仓、流动性风险，以及更高的借贷成本，需要谨慎把控。

7. 理论支持与常见问题¶

7.1 统计检验：t-统计量¶

从统计学角度，如果我们要检验一个策略的收益是否显著大于 0，就会计算 t-统计量（t-stat）。有数学推导表明：

\[ t \propto \text{Sharpe Ratio} \]

当夏普比率越高，对应的 t-stat 也越高
这意味着策略在统计学上"盈利更具显著性"，我们对它的持续盈利更有信心

7.2 学术理论：切线组合（Tangency Portfolio）¶

在现代投资组合理论（如马克维茨理论的扩展）中，如果投资者的目标是最大化收益，并最小化方差（或波动），那么最优的选择就是"切线组合"，即夏普比率最高的那条投资组合。这是在理论层面证明"夏普比率越高越好"的学理依据。

7.3 实际市场中的夏普比率水平¶

标普 500 指数（S&P 500）：长期（20 年周期）夏普比率约在 0.4~0.5 左右
巴菲特（Berkshire Hathaway）：约 0.75
优秀对冲基金：2.0 以上
极端高夏普（>5）：一般只会在小规模、特定市场环境或接近套利机会时出现，很难大规模复制

如果你能长年累月地维持 夏普比率 \(\ge 2\)，那已经超过了市场上绝大多数投资者。

8. 小结¶

收益率固然重要，但不应孤立看待，风险（波动） 同样关键。
夏普比率（Sharpe Ratio） 将收益和风险结合，是衡量"风险调整后收益"的主流指标。
分散化、对冲等手段可以让整体波动更小，大幅提升组合的夏普比率。
当一个高夏普策略本身回报不够高时，可以考虑运用杠杆来提升回报，且不降低夏普比率。
在统计学和金融学理论中，夏普比率都有坚实基础和重要地位。
长期实现 2+ 的夏普比率，已能击败绝大多数市场参与者。

希望这篇更深入的介绍能帮助你更好地理解夏普比率。追求更高夏普、打造平滑收益曲线，是许多量化交易与投资管理的终极目标。祝各位投资顺利！

后记：
- 这里使用的夏普比率多数场景中忽略了无风险收益率 \(r_f\)，因为目前很多投资环境下 \(r_f\) 相对收益远小于波动幅度。
- 真正交易中，还要考虑杠杆融资成本、交易成本、滑点、税费以及市场限制等因素，实际夏普比率也会受其影响而变化。
- 对夏普比率非常高的策略，要保持警惕性，辨别其稳健性和可持续性。

关于LLMQuant¶

LLMQuant是由一群来自世界顶尖高校和量化金融从业人员组成的前沿社区，致力于探索人工智能（AI）与量化（Quant）领域的无限可能。我们的团队成员来自剑桥大学、牛津大学、哈佛大学、苏黎世联邦理工学院、北京大学、中科大等世界知名高校，外部顾问来自Microsoft、HSBC、Citadel、Man Group、Citi、Jump Trading、国内顶尖私募等一流企业。