你真的读懂隐含波动率？量化交易员带你入门Implied Volatility¶

为了满足粉丝的入门学习需求，结合行业最新理解，LLMQuant推出量化交易员带你入门系列本文将带你从零开始了解期权隐含波动率（Implied Volatility，IV），并介绍如何基于期权数据构建波动率曲面（Volatility Surface）。文章还给出一些精要的 Python 代码示例，帮助你快速上手。

一、什么是隐含波动率？¶

在著名的 Black-Scholes 定价模型中，期权价格与波动率之间存在单调且连续的关系。于是，对于给定的期权市场价 \(V\)，总能找到一个唯一的波动率 \(\sigma^*\) 使得该模型预测价与市场价匹配。这个 \(\sigma^*\) 称作隐含波动率（Implied Volatility，IV）。

之所以称作"隐含"，是因为投资者对未来波动程度的所有预期最终都反映到期权实际交易价格上，而反算回来的 \(\sigma\) 就成了市场"共同认可"的平均波动率判断。

二、波动率曲面：两维空间的 IV¶

当我们在同一标的下，有不同行权价 \(K\) 和不同到期时间 \(T\) 的期权，对应各自的隐含波动率，就能用三维方式去可视化：

x轴：Strike（行权价）
y轴：Time to Maturity（到期时间或剩余天数）
z轴：Implied Volatility

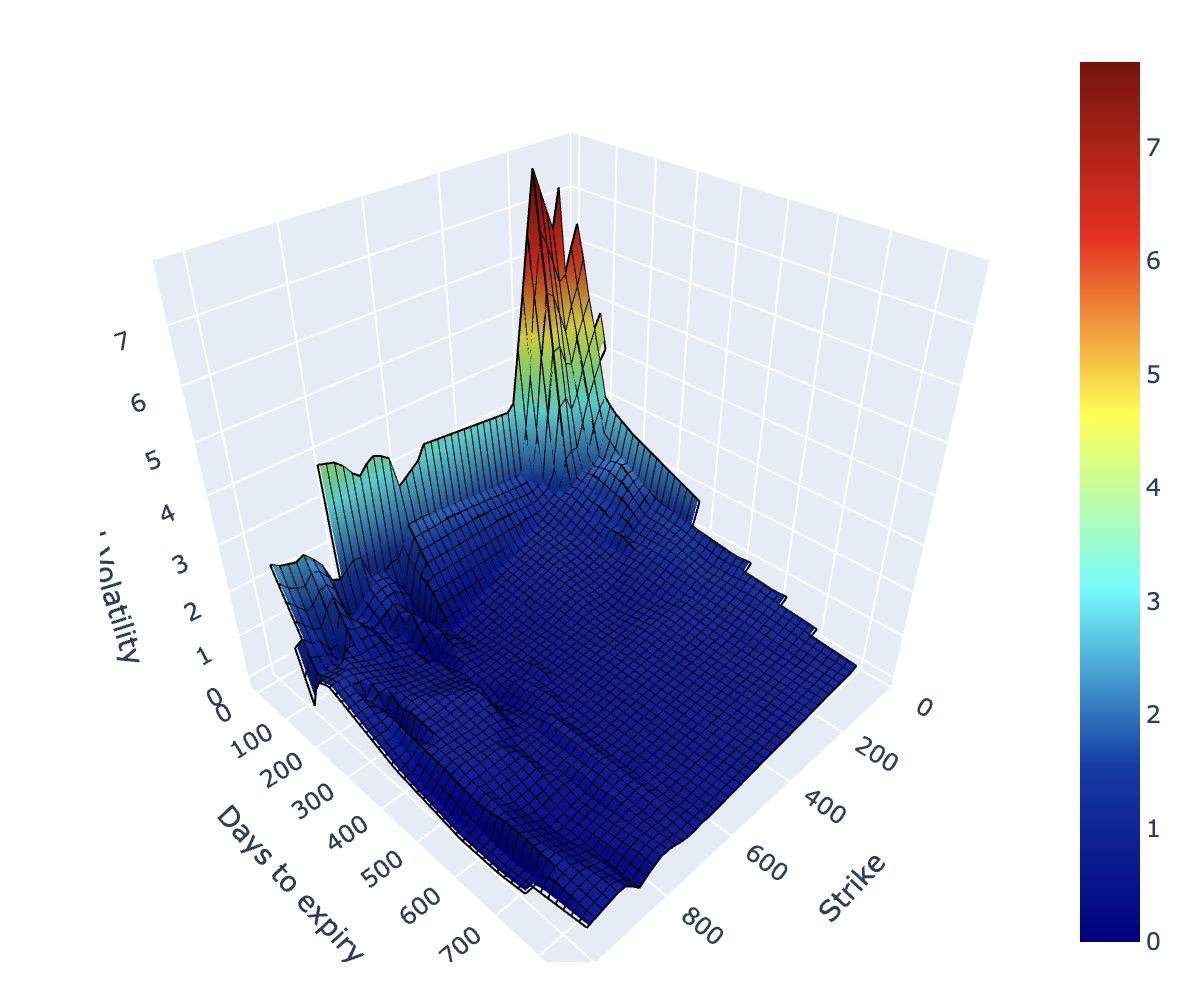
将它绘成三维图，就得到所谓的波动率曲面（Volatility Surface）。该曲面提供了更直观的信息，让我们能快速捕捉市场对未来不同到期点、不同价位的波动预期。

三、如何获取期权数据¶

在 Python 中，常用 yfinance 直接从 Yahoo Finance 获取期权数据。以下是一个简要示例：

import yfinance as yf
import pandas as pd

def get_options_data(ticker):
    """获取完整的期权链信息并合成为一个DataFrame。"""
    yf_ticker = yf.Ticker(ticker)
    expiry_dates = yf_ticker.options  # 列出所有到期日

    options_data = pd.DataFrame()
    for expiry in expiry_dates:
        chain = yf_ticker.option_chain(expiry)
        call_df = chain.calls.assign(call=True)
        put_df = chain.puts.assign(call=False)
        merged = pd.concat([call_df, put_df])
        merged["Expiration"] = pd.to_datetime(expiry)
        options_data = pd.concat([options_data, merged], ignore_index=True)

    return options_data

# 示例：获取苹果 (AAPL) 的期权数据
aapl_options = get_options_data("AAPL")
print(aapl_options.head())

获取后，我们即可查看每份期权的行权价、bid/ask价格、剩余到期日等，为后续计算隐含波动率做准备。

四、数值计算隐含波动率¶

4.1 Black-Scholes 回顾¶

Black-Scholes 看涨期权价格大致如下（简化形式）：

\(C = S_t \Phi(d_1) - K e^{-r (T - t)} \Phi(d_2)\)

其中

\(d_1 = \frac{\ln(S_t/K) + (r + 0.5\,\sigma^2)\,(T-t)}{\sigma \sqrt{T-t}}\)，
\(d_2 = d_1 - \sigma \sqrt{T-t}\)，

\(\Phi\) 为标准正态 CDF。看跌期权可用 put-call parity 推出类似公式。

4.2 隐含波动率：求根问题¶

若给定期权市场价 \(V\)，则隐含波动率是满足 \(C(\sigma) - V = 0\) 的 \(\sigma\)。常用求解方法包括二分法（Bisection）、Newton-Raphson 和 Brent 等。本科普简单演示下二分法的实现：

import numpy as np

def black_scholes_call_price(vol, S, K, T, r):
    """简化版BS看涨期权定价（到期时间已折算为年化）。"""
    from scipy.stats import norm
    if vol <= 0: 
        return 0.0  # 波动率不可能小于等于0
    d1 = (np.log(S/K) + (r + 0.5*vol**2)*T) / (vol*np.sqrt(T))
    d2 = d1 - vol*np.sqrt(T)
    return S*norm.cdf(d1) - K*np.exp(-r*T)*norm.cdf(d2)

def implied_vol_bisection(market_price, S, K, T, r, lower=1e-5, upper=5.0, tol=1e-6):
    """通过二分法求解隐含波动率。"""
    for _ in range(100):  # 最多迭代100次
        mid = 0.5*(lower+upper)
        price = black_scholes_call_price(mid, S, K, T, r)
        if abs(price - market_price) < tol:
            return mid
        if price > market_price:
            upper = mid
        else:
            lower = mid
    return 0.5*(lower+upper)

# 示例：行权价K=100，市价5，标的现价S=102，期限T=0.25年，r=2%
iv_est = implied_vol_bisection(market_price=5, S=102, K=100, T=0.25, r=0.02)
print("隐含波动率(估计)：", iv_est)

实际场景中，可以改用更快收敛的 Newton-Raphson 或使用不需要导数的 Brent 算法。

五、构建与可视化波动率曲面¶

遍历期权表：对每个期权记录（行权价、到期日、市场价…）调用前述函数，计算隐含波动率。
整理数据：将 \((K, T)\) 对应的 \(\sigma\) 存起来。对一些深度实值或数据异常的期权可过滤。
插值与绘图：
在二维平面（\((K,T)\)）上做网格；
用插值（LinearNDInterpolator、Cubic Spline 等）获取网格每点的 IV；
用三维或等值线图可视化。

以下仅演示线性插值思路（代码省略数据来源等）：

from scipy.interpolate import LinearNDInterpolator
import numpy as np
import plotly.graph_objects as go

# 假设我们已有(Strike, TTE, IV)三个数组
strike_vals = np.array([...])
time_vals   = np.array([...])  # Time to Expiry
iv_vals     = np.array([...])

# 1) 构建插值器
points = np.column_stack((strike_vals, time_vals))  # shape: (N,2)
lin_interp = LinearNDInterpolator(points, iv_vals)

# 2) 网格
K_grid = np.linspace(min(strike_vals), max(strike_vals), 50)
T_grid = np.linspace(min(time_vals), max(time_vals), 50)
KK, TT = np.meshgrid(K_grid, T_grid)

# 3) 获取插值值
IV_surface = lin_interp(KK, TT)

# 4) Plotly可视化
fig = go.Figure(data=[go.Surface(x=KK, y=TT, z=IV_surface)])
fig.update_layout(title="Volatility Surface", 
                  scene=dict(
                      xaxis_title="Strike", 
                      yaxis_title="Time to Expiry", 
                      zaxis_title="Implied Vol"))
fig.show()

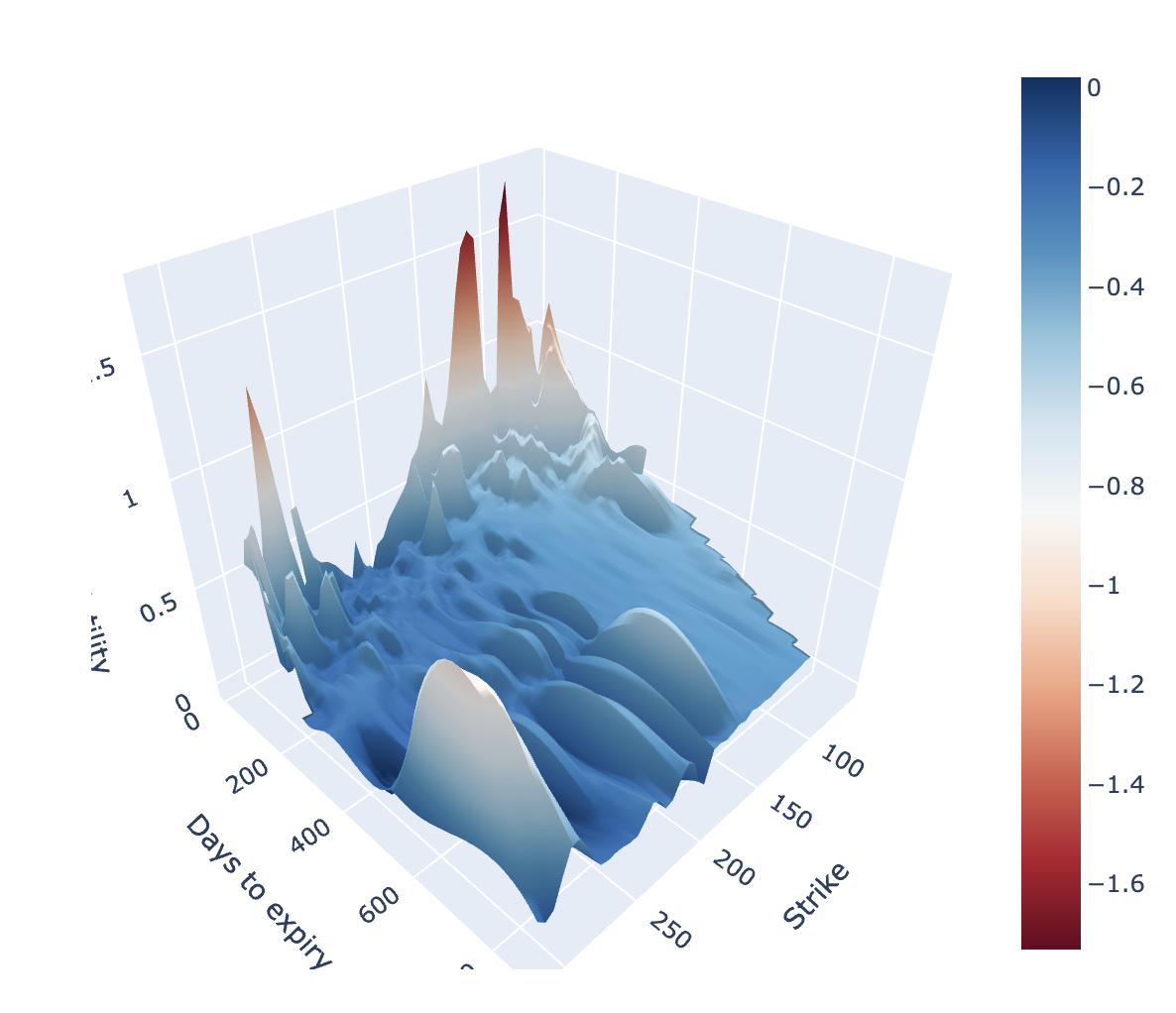
六、常见特征：Skew、Smile 与期限结构¶

Skew（偏斜）：在某固定到期日上，若行权价较低（深虚值看跌）的 IV 明显高于平值，形成负偏斜；反之则正偏斜。
Smile（微笑）：两端远离平值处的期权 IV 高于中间，形成"微笑形状"。
Term Structure（期限结构）：同一行权价下，短期 IV 与远期 IV 可能并不一致，甚至出现先升后降等形态。

七、注意事项与扩展¶

深度实值期权：价差大或成交稀少，隐含波动率不稳定。
数据准确性：若 bid/ask 均为 0 或相差很离谱，需谨慎对待。
无套利：线性或样条插值易导致日历套利或蝶式套利。对专业需求，最好使用 SVI、SSVI 等模型。
速度优化：大规模计算 IV 时，可用近似公式或混合牛顿法加速。

八、总结¶

隐含波动率与波动率曲面是期权交易及风险管理的核心。通过获取期权链、数值求解 IV、插值并可视化，我们能对市场对未来的波动预期一览无余。要让曲面更贴近真实且无套利，还需更专业的模型与调优。

希望本文能为你提供一个快速上手的路径，也欢迎探索更多高级主题（Bachelier、SVI、机器学习），让"波动率曲面"在量化策略中大展身手。

参考阅读
- Gatheral, J. & Jacquier, A. (2013). Arbitrage-Free SVI Volatility Surfaces. SSRN.
- Jaeckel, P. (2010). By Implication.
- Choi, J., Kwak, M., Tee, C.W., Wang, Y. (2021). A Black-Scholes user's guide to the Bachelier model. arXiv.

关于LLMQuant¶

LLMQuant是由一群来自世界顶尖高校和量化金融从业人员组成的前沿社区，致力于探索人工智能（AI）与量化（Quant）领域的无限可能。我们的团队成员来自剑桥大学、牛津大学、哈佛大学、苏黎世联邦理工学院、北京大学、中科大等世界知名高校，外部顾问来自Microsoft、HSBC、Citadel、Man Group、Citi、Jump Trading、国内顶尖私募等一流企业。